İkizkengen üçgeninin alanını nasıl bulurum?

Matematik ve geometri, özellikleen sevilmeyen derslerden biri olan okul çocuklarının anketleri ve hepsi hayatta% 80 oranında mevcut yetişkinlerin pratik başvuru bulamadıklarını çok sayıda formül öğrenmelerini sağladığı için yaptı. Fakat, bir dakikalığına formülleri öğrenir, sorunları çözer, hayatta bizim için yararlı olabileceği için değil, düşünce ve mantığı geliştirdiği için denklemler yaparız. Hatta eski Yunan bilge, insan aklının matematik bilimleri bilgisi ile ölçülebileceğini söyledi. Ve bir ikizkenar üçgen için formüllerin uygulanması hakkında bilgi vermeye karar verdiğinizden beri kendimizi elimize alıp makalenin tamamını okuyun.
Soruyu cevaplamaya başlamadan önce nasıl bulacağınızikizkenar üçgeninin alanı ve formülün ve hesaplamaların verildiği makalenin pratik bölümüne gidin, kendimiz için olan kavramı belirtelim. İkizkenar üçgen üç kenardan ikisinin uzunluğuna eşit olan ve yan taraf olarak adlandırılan bir üçgentir. Normal bir üçgen durumunda, tüm kenarların eşit olduğu durumda, ikigen izoleli olarak da kabul edilir, ancak tam tersi olarak, bir iki köşeli üçgen doğru kabul edilirse - yanlış olur.
Üçgenin kenarları belirlenmelidir, bunu aşağıdaki şekilde gösterildiği gibi yapacağız, burada: a - kenarlar, b tabanı ve yükseklik.
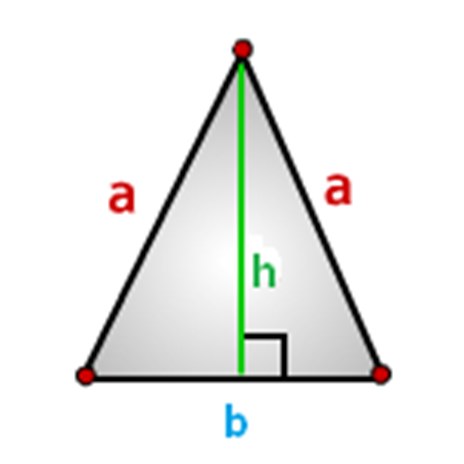
İkizkengen üçgeninin alanını hesaplamak için formüller.
Yükseklik, yan ve açı notasyonlarını yaptıktan sonra sorunu çözmeye başlayabiliriz.
Öncelikle, bildiklerini belirleyeceğiz.
Yükseklik ve alt - o zaman klasik formül (* - çarpım işareti):
S = ½ * b * h
Örneğin, sayıların yerini alalım: h = 16, b = 18, şunu elde ederiz:
S = ½ * 18 * 16 = 9 * 16 = 144;
İkizkenar üçgeninin alanı S = 144 cm2'dir
Bize yardımcı olacak başka formüller varikizkenar üçgeninin alanını bilmek. Böyle bir formül Heron'un yöntemi. Karmaşık bir formül yazmayalım, temelde kısaltılmış olarak alıyoruz:
S = ¼ b √4 * a2-b2
Taban ve - - Eşit taraflar O b açıktır. h yüksekliği bilinmediğinde formül uygundur.
Değerlerin yerini alsak, a = 6, b = 3 olsun, şunu elde ederiz:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Üçgenin kenarlarına ve kenarların arasındaki açıya eşit alanı hesaplamak için kullanabilirsiniz:
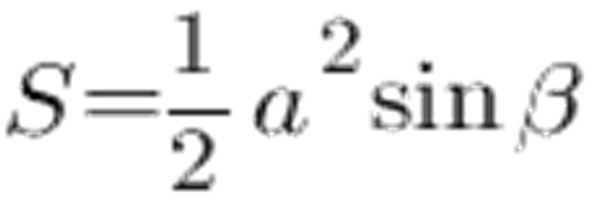
Sinüs tablosuna göre, 45 ° açısı 0.7071, a kenarı a ve 6 cm olsun, aşağıdakileri elde ederiz:
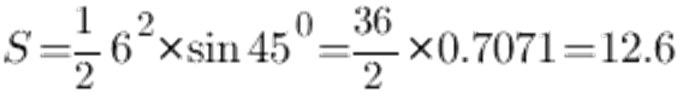
Sonuç olarak, ikizkenar üçgeninin alanı 12.6 cm2'dir.
Alanı hesaplamak için aşağıdakileri de içeren yollar vardır:ikizkenar üçgenler de dahil olmak üzere, ancak karmaşıktır ve yukarıda verilenler gibi "temel" hesaplamalara karmaşık matematik kavramında uygulanmazlar. Deneyimli öğretmenler bile anlayamayacak şeyler hakkında konuşmaya değmez.
Yani, bu konuda rahat bir nefes alabilirsinbir ikizkenar üçgeninin alanını bulmak için bir geometri çizgisi eksiksiz olarak kabul edilecek ve makaleyi okumanın sonucu olarak elde edilen bilgi "beş" ile öğrenilir.